(Maderuelo, Segovia; España). Foto: Cristina Martínez García
En este post te propongo tres problemas relacionados con ángulos inscritos en la circunferencia. El primero es de carácter teórico; los otros dos son aplicaciones del primero. Como viene siendo habitual en este blog ambos pueden calificarse de sencillos.
Algunas cuestiones que debes saber son:
1) Toda recta tangente a una circunferencia es perpendicular al radio correspondiente al punto de tangencia.
2) La suma de los ángulos de un triángulo vale 180º.
3) Las propiedades de los triángulos isósceles: dos lados iguales y ángulos opuestos a ellos también iguales.
Problema 1
Demuestra que el ángulo inscrito en una circunferencia, determinado por un lado secante y otro tangente a la circunferencia, vale la mitad que el ángulo central correspondiente. Esto es: la medida del ángulo BAC es la mitad que la del ángulo AOC. (Véase la siguiente figura).
Problema 2
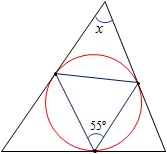
En la siguiente figura la circunferencia dada es inscrita al triángulo grande y circunscrita al pequeño. Si el ángulo dado mide 55º, ¿cuánto mide x?
Problema 3
La circunferencia de la figura es tangente a la recta horizontal en el punto A y las cuerdas BA y BC tienen la misma longitud. La prolongación de la cuerda BC corta a la recta en el punto D. Si el ángulo en A vale 70º, ¿cuanto mide x?