Geometría (99). Triángulos equiláteros

Foto: Adrián Santos

IX CONCURSO DE PRIMAVERA DE MATEMÁTICAS (2005, Nivel IV, 2º Fase)
https://www.concursoprimavera.es/resources/problemas/problemas-2005-fase2-nivel4.pdf

El problema que sigue se planteó a los alumnos de Bachillerato en el Concurso de Primavera. Su solución es muy fácil aplicando la noción de seno de un ángulo. Y es más fácil si se piensa un poco, cosa que no ha hecho el que suscribe; aunque después he completado el asunto.
Mi solución no coincidía con ninguna de las cinco dadas en el examen, pero dadoel cuidado con el que preparan las pruebas los organizadores del Concurso me he planteado hacerlas coincidir. Así ha sido; pero después, pensando un poco más, he dado con la solución casi inmediata, supongo que erala prevista por los organizadores.

Problema
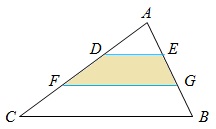
El triángulo ABC de lados correspondientes a, b y c tiene un ángulo en A de 120º. Por ello podemos obtener girando, el triángulo equilátero BCD formado por tres triángulos como el de partida y un triángulo equilátero pequeño interior AEF. ¿Cuál es el área de este triángulo equilátero AEF?

Solución.

Geometría (98). Con compás (I)

Foto: Antonio Martínez García

El problema que planteo es un clásico "de regla y compás". En estos problemas es frecuente que “la idea” sea decisiva. Y más frecuente aún es que cuando esté resuelto parezca una obviedad. Algo de eso pasa aquí. Se trata de un problema sencillo cuando se ha resuelto.
Puede proponerse a los alumnos de bachillerato, aunque podría ponerse desde 2º de ESO, pues los conocimientos que se precisan son elementales para los seguidores de este blog: teorema de Tales; perpendicularidad; paralelismo…; que la distancia de un punto a una recta es la menor de las distancias posibles, la que hay entre el punto dado y su proyección (perpendicular) sobre la recta.
Por cierto, hay dos soluciones.

Problema
Dado un punto A sobre el lado r de un ángulo, encontrar otro punto B en el mismo lado que equidiste de A y del otro lado s.

Solución.

Geometría (97). Trapecio

Foto: Carmen García Matas (Parque de El Retiro, Madrid)

XXV JORNADA MATEMÁTICA VALENCIA GUADALAVIAR 2016 (3º de ESO, 2ª Fase)
http://colegioguadalaviar.es/jornada-matematica-valencia/#pruebas

Casi desconocida por mi, la Jornada Matemática Valenciana ha reunido en el último año a más de 3000 escolares en sus distintos niveles: desde Primaria hasta Bachillerato. Pienso que hay que felicitar a los organizadores del evento. Es bueno que los estudiantes, desde pequeños se acostumbren a ver las matemáticas como algo estimulante.

El problema que he elegido se propuso a los participantes de 3º de ESO. No tiene especiales dificultades y, además, puede hacerse de varias formas. Por tanto, ánimo.

Problema
¿Cuál es la altura de un triángulo que resulta prolongando los lados no paralelos de un trapecio cuyas bases son de 27 m y 38,50 m y su altura 15 m?

Solución.

Geometría (96). Semejanza/Áreas

Foto. Cristina Martínez García

https://www.concursoprimavera.es/resources/problemas/problemas-2006-fase2-nivel3.pdf

Continúo con el mismo asunto que en el post 95. Se trata de otro problema sencillo, que se resuelve aplicando la relación de proporcionalidad, tanto en longitudes como en superficies. Como dije en el post anterior, puede ser apropiado para alumnos de 3º de ESO.

Problema
ABC es un triángulo equilátero y los puntos D, E, F, G, H, I dividen a los lados en tres partes iguales. ¿Cuál es el cociente entre el área del cuadrilátero DFGH y el triángulo ABC?

Solución.

Geometría (95). Semejanza/áreas

Foto: Adina Marín (Vaticano)

https://www.concursoprimavera.es/resources/problemas/problemas-2006-fase2-nivel3.pdf

En este post se propone otro problema sencillo. Se trata de aplicar la relación de proporcionalidad, tanto en longitudes como en superifices. Por tanto puede plantearse a los alumnos de 3º de ESO, pues en ese curso se estudian ambos conceptos.

Problema
En el triángulo ABC de la figura, de área 90 cm2, los puntos E y G dividen al lado AB en tres partes iguales y las rectas DE y FG son paralelas a BC. ¿Cuál es, en cm2, el área del trapecio DEGF?

Solución.

Geometría (94). Tangentes exteriores

Foto: Antonio Martínez García (En la ermita de Hornuez, Segovia)

https://www.concursoprimavera.es/resources/problemas/problemas-2005-fase2-nivel4.pdf
 

Como había anunciado en el post anterior (Geometría 93), vuelvo con otro problema sencillo. Los conocimientos necesarios para su resolución son los mismos: Tales, Pitágoras; y la propiedad de la tangente a una circunferencia.

Problema
Las dos circunferencias de la figura son tangentes exteriores y las rectas PAB y PA’B’ las tangentes comunes a ambas. Si PA = AB = 4, ¿cuánto mide el área del círculo pequeño?

Solución.

Geometría (93). Tales (otro)

Foto: Carmen Martínez García (un río noruego)

file:///C:/Users/Usuario/Downloads/problemas-2005-fase2-nivel3%20(1).pdf

Cuando propongo los problemas de este bolg a mis alumnos siento que les cuesta una barbaridad su resolución. Por eso, cuando comienzo estos posts con la “coletilla” de “el problema que propongo a continuación es relativamente sencillo”, no terminan de creerme. Pero ellos deben tener razón: no les resulta fácil.
Precisamente, la falta de conocimientos geométricos de los estudiantes de Secundaria, (de todos, de ESO y de Bachillerato), fue lo que me llevó a iniciar este Blog y a proponer estos problemas “sencillos”. Supongo que algo estaré aportando.
Pero esta vez es verdad: el problema siguiente es muy fáciles (y lo mismo haré en el siguiente). Espero que así se anime más de uno a resolverlos. Solo hay que conocer dos cosas: el de Tales y la propiedad de la tangente a una circunferencia. Por tanto, ¡ánimo!

Problema
Los radios de dos circunferencias concéntricas están en la razón 1 a 3. Si AC es un diámetro de la circunferencia grande, BC una cuerda de la grande tangente a la pequeña y AB = 12, ¿Cuánto vale el radio de la circunferencia grande?

Solución.

Geometría (92). Sin huecos (II)

Foto: Carmen García Matas (Guadalquivir por Córdoba)

Este post es una continuación del anterior (Geometría, 91). Allí se propuso un caso particular del problema general de “rodear un polígono regular de m lados por m polígonos regulares de n lados cada uno, sin que haya huecos ni superposiciones”. En concreto, se pedía: ¿Cuánto vale n si m = 10? La solución era que n = 5. Más abajo se dibuja la solución.

El lector interesado puede comprobar que una disposición de polígonos cumpliendo las exigencias anteriores generan diversos tipos de mosaicos. (La fotografía de portada del post 90 muestra uno de ellos). En la solución de este problema pueden verse algunos bocetos que he realizado.

Pero el problema que planteo es otro; es la demostración de que solo hay cuatro posibilidades de unir polígonos regulares en las condiciones descritas.  

Problema
Demuestra que solo hay cuatro soluciones para m de “rodear un polígono regular de m lados por m polígonos regulares de n lados cada uno, sin que haya huecos ni superposiciones”. En la imagen se muestra un polígono regular de 10 lados rodeado por 10 pentágonos regulares. (En el post anterior se da otro dibujo para m = 4).

Solución.